2022-2023全国100所名校数学卷六 答案

2022-2023全国100所名校数学卷六 答案，全国100所名校答案网已经编辑汇总了2022-2023全国100所名校数学卷六 答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

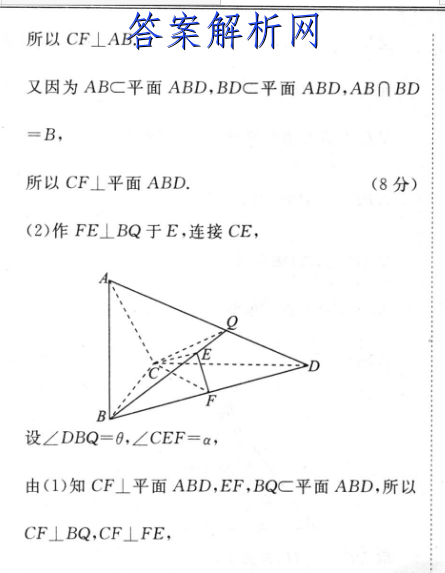
11.解：(1)因为BC=CD,F为线段BD中点，所以CF⊥BD因为AB⊥平面BCD,CFC平面BCD,所以CF⊥AB.又因为ABC平面ABD,BDC平面ABD,AB∩BD=B,所以CF⊥平面ABD.(8分)(2)作FE⊥BQ于E,连接CE,B设∠DBQ=O,∠CEF=a,由(1)知CF⊥平面ABD,EF,BQC平面ABD,所以CF⊥BQ,CF⊥FE,又EF∩CF=F,所以BQ⊥平面EFC,ECC平面EFC,所以BQ⊥EC,所以∠CEF为二面角D一BQ一C的平面角(12分)因为二面角D一BQ-C与二面角A一BQ一C为互补二面角，(14分)所以d cos a =34,tan a=CF2sin音EF2cos6·sind13 sin 0所以=后n。于是n0=市im(受-0)√3sin0=23√13SADBQ合·QB·BD·sin0AS△aBA合·QB·BA·sin(受-O）23.11313.253(18分)√13所以器=，即的值为(20分)

【解析】由题意，在平面BCD内作BQ⊥CD,交CD于Q,因为平面BCD⊥平面ACD,平面BCD与平面ACD交于CD,所以BQ⊥平面ACD,又BP⊥平面ACD,所以P,Q两点重合，于是随着点D的变化，BP⊥CD始终成立，可得在平面ABC中，BP⊥CP始终成立，即得点P的轨迹是以BC为直径的圆的一部分，由题意知随着点D的变化，∠BCD的范围为[0,受]，可得点P的轨迹是以BC为直径（半径为1)的圆的3，即得点P的轨迹长度为3×2x×1=23元，