全国100所名校卷答案理数

全国100所名校卷答案理数，全国100所名校答案网已经编辑汇总了全国100所名校卷答案理数的各科答案和试卷，更多全国100所名校答案请关注本网站。

2020全国100所名校理综卷答案八

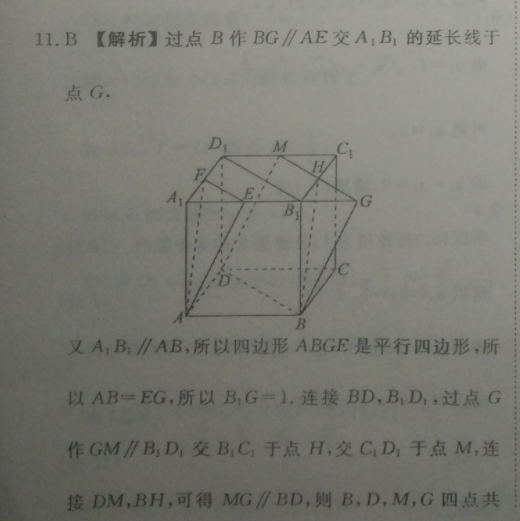
11.B【解析】过点B作BG∥AE交A,B,的延长线于点G,又A,B,∥AB,所以四边形ABGE是平行四边形，所以AB=EG,所以B,G=L.连接BD,B,D,过点G作GM∥BD,交BC,于点H,交CD1于点M,连接DM,BH,可得MG∥BD,则B,D,M,G四点共面，可知BG∥平面AEF,GM∥平面AEF,文BGOGM=G,所以平面BDMG∥平面AEF,所以四边形BDMH为所求截面，可知四边形BGMD为平行四边形，H为B,C的中点，所以GH=√2，又BH=√B,+BB=√5=BG,所以△BGH的面积S=是GH·√BF-(y=合×E×√5)”-（号）=是，所以四边形BDMH的面积为35=3×号-号故选B,

全国100所名校单元测试示范卷语文二十一

10.D【解析】易知a2=一2，由a.4+1=(一2)”，得a+1a+2=(一2)+1，相除得a+2=一2，所以数列{a,}的所有奇数项构成以1为首项，一2为公比的等比数列，所有偶数项构成以一2为首项，一2为公比的等比数列，所以S2m=(a1十a1十…十a2-1)十a+a+…+a)=二二+二221-(-2)=一2）”1所以9-5.--（-2-3(-2)=一2)1.若m为偶数，则S.3（-2)号-1，所以135.+1=2>2022，又m∈么，3解得n≥22，此时n的最小值为22；若m为奇数，则S.-（-2)学-1，所以135.+1=2岸>2022，又3m∈Z,所以m≥19，此时m的最小值为19.故选D.